解读FM合成器『6』--FM与滤波器

解读FM合成器『6』--FM与滤波器
让咱们继续,先说说带宽(bandwidth)的问题,其实在式子6里面已经涉及到他了。
上一讲提到的式子6,还没有忘吧:
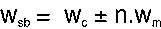
当时我说了,理论上边带一直向两个方向延伸(因为n可以取任意的整数值),但实际应用上不可能实现无限的边带,也就是说带宽不可能是无限的,那么在现实的应用里FM的信号到底是什么样子的呢?
带宽就是波形发生后,波形所占据的频率范围。比如说一个非常精确的100Hz的正弦波,他的带宽基本上可以忽略不计,但是如果我们给这个正弦波加上一个200Hz的谐波,那么这个正弦波就会产生100Hz的带宽。同样的一个信号如果占用了100Hz到1500Hz,那么他的带宽就是1400Hz。让我们带着这个概念来看看FM的输出。
假设载波器是一个500Hz的正弦波,调制器是一个300Hz的正弦波,你将他们使用调音台简单的混合在一起,使用上面的理论,那么他的带宽应该是200Hz。
如果我们用振幅调制的观念来看,他的三个特殊成分分别是Wc、Wc+Wm、Wc-Wm,那么数值应该分别是500Hz、800Hz、200Hz。所以由此看来带宽又应该是最低频率与最高频率的差值:600Hz。
那么FM信号的带宽是怎么样的?虽然理论上说边带是无限的,但是调制指数使得n在取到比较大的数值之后的振幅可以忽略不计了。这里有一个凭着经验得出的公式,这就是式子8:
式子8:
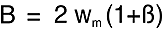
B表示被调制的带宽,Wm是调制频率,β是调制指数。
还是举上面的例子,假设载波器是一个500Hz的正弦波,调制器是一个300Hz的正弦波,β是一个很小的数(近似于0),那么带宽应该是2X300HzX(1+0)=600Hz。所以说当β比较小时,带宽可以近似等于振幅调制的带宽。
但是如果β变大了,比如说β=5时,这时的带宽就是2X300HzX(1+5)=3600Hz。很明显,β越大,带宽就越宽,FM信号就越复杂。看下图(Figure12),红线表示带宽的宽度,蓝线表示输出中的特殊成分,看到了吧信号简单的混合的带宽最窄,振幅调制和当β=0.1(很小)频率调制拥有差不多宽的带宽,而β=5时的频率调制的带宽最长。注意到特殊成分了吗?β=5时的频率调制足足有24个离散的特殊成分(蓝线),想知道为什么吗?我们下一讲再解释这个复杂的问题,毕竟这一讲我们的重点在FM的滤波问题上。
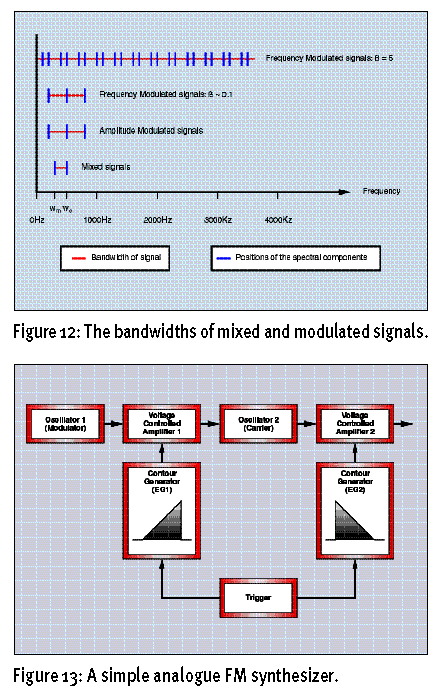
在减法合成器里,音量的变化通常都要使用振幅包络发生器,同样的任何音调的改变都要使用滤波器的截止频率包络发生器。在FM里面,音量的变化同样由声音信号的音量包络决定,但是音调的改变却再也不需要滤波器。因为调制器的振幅决定着输出信号的带宽,请看上图(Figure13)。
当图中的EG2(Envelop Generator包络发生器)使得VCA2(压控放大器)减小时,输出的振幅也减小了,也就是说输出的声音变的越来越小。同时呢EG1的增加使得由VCO1(压控振荡器)带动的调制信号的最大振幅也增加了。也就是说调制指数变大了,带宽更宽了,由此声音变的越来越明亮(这和自然生活里音量越大声音越明亮的现实完全相反)。这样就会使声音的声调改变了,也许你还不甘心,非要使用滤波器来改变声音的音调,虽然为声音加上一个低通滤波器会使声音的声调改变,但是遇到频率调制的音色,滤波器会显得无能为力。
本文参考Sound On Sound的《Synth secrets--PART 12: AN INTRODUCTION TO FREQUENCY MODULATION》一文编译,有说的不对的翻译的不准确的望您指出
文章出处 midifan
转载文章请注明出自 Midifan.com




